Berechnung der Standardabweichung

Die Standardabweichung kompensiert den Nachteil der Varianz, indem sie aus der  Quadratwurzel der Varianz gebildet wird und somit dieselbe Einheit wie die Daten besitzt. 
Wie bei der Varianz ist zu unterscheiden zwischen der Standardabweichung, die die gegebenen Daten charakterisiert

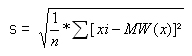
und der Standardabweichung, die aus Stichprobendaten als Schätzwert für die Grundgesamtheit berechnet wird

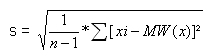
Es gilt also:

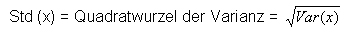
Für das Beispiel gilt:

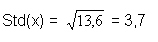
Mathematische Bedeutung
Liegt eine Beobachtungsreihe (x1, x2,…,xn) der Länge N vor, so sind empirischer Mittelwert und empirische Standardabweichung die zwei wichtigsten Maßzahlen in der Statistik zur Beschreibung der Eigenschaften der Beobachtungsreihe.

Die Standardabweichung heißt auch mittlerer Fehler oder RMS error (von engl. root mean square). Als Abkürzung findet man neben σ in Anwendungen oft auch s, m.F. oder englisch rms. In der angewandten Statistik findet man häufig die Kurzschreibweise der Art „Ø 21 ± 4“, was als „Mittelwert 21 und Standardabweichung 4“ zu lesen ist.

Interpretation
Aus Angaben zu Mittelwert und Standardabweichung ergibt sich die mittlere Schwankungsbreite (gilt im Falle normalverteilter Mengen, wovon man bei zufälligen und ausreichend großen Stichproben ausgehen kann).

Es gilt:
Im Bereich von „Mittelwert ± 1 Standardabweichung“ befinden sich ca. 68% aller Teilnehmer der Grundgesamtheit

In unserem Beispiel: MW(x) ± 1*std(x) = 23,5 ± 3,7 = 19,8 bzw. 27,2 Jahre

Bei einer repräsentativen und ausreichend großen Stichprobe könnte man den Schluss ziehen, dass 68% aller Teilnehmer der Grundgesamtheit zwischen 19,8 und 27, 2 Jahre alt sind.

Weiter gilt:

• Im Bereich Mittelwert ± 2*Std(x) befinden sich ca. 95% der Teilnehmer
• Im Bereich Mittelwert ± 3*Std(x) befinden sich ca. 99% der Teilnehmer

Faustregel für die Praxis
Werte außerhalb der zwei- bis dreifachen Standardabweichung nennt man Ausreißer. Viele Ausreißer können ein Hinweis auf grobe Fehler der Datenerfassung sein.